Duemila anni dopo che il matematico e poeta indiano Acharya Pingala la descrisse per la prima volta, la sequenza di Fibonacci sta ancora comparendo in posti nuovi. La serie, in cui ogni numero è la somma dei due precedenti, porta il soprannome del matematico italiano che lo introdusse in Europa, Leonardo Bonacci (“Fibonacci” significa “Figlio di Bonacci”). Di recente, gli scienziati hanno scoperto che la sequenza (0, 1, 1, 2, 3, 5, 8, 13 … ) si mappa magnificamente su alcuni dei sistemi più complessi in natura, offrendo un indizio allettante sui meccanismi della crescita biologica.
Michael Simon Toon non era alla ricerca di questi numeri famosi quando iniziò a progettare alberi sintetici per un progetto di energia solare . Toon ha notato che sebbene esistano altri progetti di alberi solari, nessuno aveva ancora replicato con successo la stabilità strutturale e l’efficienza della superficie che gli alberi naturali usano per raccogliere l’energia luminosa. L’ispirazione per la versione di Toon è venuta da un’altra antica intuizione: la regola ampiamente accettata di conservazione dell’area di Leonardo da Vinci , che postula che la somma dello spessore di tutti i rami di un albero non può superare lo spessore del tronco.
Artista, designer e appaltatore con sede a Los Angeles, in California, Toon aveva già incontrato il potere della bellezza matematica nei suoi apparecchi di illuminazione e nei progetti di edifici modernisti, quindi l’idea di basare un progetto di ispirazione biologica su un’antica legge della botanica si è resa perfetta senso. “Avevo già visto progetti solari a forma di albero , ma non assomigliavano per niente a veri alberi”, dice a Popular Mechanics . Soprattutto, non erano realistici: “Non vedi mai un albero simmetrico”.
Per costruire il suo modello, Toon ha pianificato di adattare tubi di alluminio di alcune dimensioni standard (tra 1 e 4 pollici di diametro) in connettori personalizzati stampati in 3D con tre aperture. I connettori, o “cavalli” in gergo botanico, sarebbero responsabili di rendere l’albero conforme alla regola di da Vinci bilanciando attentamente le dimensioni relative dei fori dei tubi.
Per creare una forma ad albero realisticamente asimmetrica, Toon ha costruito i tre fori di ciascun connettore in tre diverse dimensioni. “Hai un unico tronco che esce dal terreno e si divide in due rami più piccoli in un albero. Un ramo è leggermente più piccolo del tronco stesso e l’altro è più piccolo del tronco o dell’altro ramo”, spiega. In altre parole, ogni connettore di ramo in questo modello di albero biomeccanico collega tre rami di diverse dimensioni, con il più grande in basso e i due più piccoli in alto.
Toon pensava che l’incorporazione di un’intuizione botanica di 550 anni avrebbe prestato al suo modello parte della bellezza e della resilienza strutturale di un albero naturale. Quello che non si aspettava era di scoprire una nuova istanza della sequenza di Fibonacci nel suo progetto
“Tutto quello che ho fatto è stato creare tutti i rami degli alberi necessari per completare l’albero, quindi ho contato il numero di cavallotti di ogni dimensione di cui avevo bisogno”, ricorda Toon. “Ed ecco, era la sequenza di Fibonacci.”
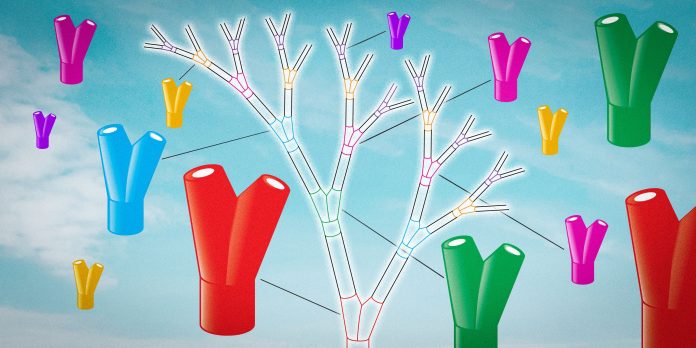
Poiché l’albero è costruito dal tronco in su, le dimensioni dei connettori dei rami diminuiscono. Per accogliere i rami tubolari, ogni cavallo deve condividere da una a tre dimensioni dei fori con un altro cavallo. Quindi, ad esempio, il primo connettore ha il foro più grande (inferiore) abbinato alla larghezza del tronco dell’albero, mentre i fori di dimensione media e più piccola sulla parte superiore hanno ciascuno la stessa dimensione di uno dei fori inferiori sul connettore più alto successivo .
In quel momento è apparsa la sequenza. Toon ha scoperto che, date queste relazioni fisse – la regola di da Vinci, i rapporti disuguali fissi delle dimensioni dei fori in ciascun connettore e la necessità di far corrispondere la dimensione del foro inferiore di ciascun connettore con una delle dimensioni del foro superiore del connettore più basso successivo – la frequenza di ogni dimensione di connettore che ha stampato seguirebbe la sequenza di Fibonacci. Se dovessi etichettare ogni connettore in base alla dimensione, ci sarebbe uno dei connettori più grandi (taglia A), uno di taglia B, due di taglia C, tre di taglia D, cinque di taglia E, otto di taglia F e così via su.
Le sequenze di Fibonacci sono ben documentate nelle spirali di alcuni petali di fiori e sono state riportate in altri sistemi di ramificazione naturali, come fiumi , radici e bronchi . Nonostante la loro fama e ubiquità, tuttavia, nuovi esempi di numeri in natura non compaiono tutti i giorni.
Regolarità strutturali come questa possono emergere naturalmente nelle forme viventi a causa delle esigenze di sopravvivenza biologica . Tutti gli alberi hanno le stesse priorità – l’utilizzo di un’energia minima per trasferire acqua e sostanze nutritive tra le radici e la chioma, senza essere rovesciati – e gli stessi materiali disponibili con cui raggiungerli, quindi l’ottimizzazione delle risorse per la sopravvivenza li costringe a una gamma limitata di architetture possibili . Il risultato è l’adesione a leggi matematiche come quella di da Vinci e l’emergente sequenza di Fibonacci Toon che si trova negli alberi biosintetici.
Le implicazioni di questa scoperta sono difficili da prevedere. Da una prospettiva scientifica, osservazioni come quella di Toon possono aiutare a guidare la ricerca sui modelli di crescita delle piante originarie. Un modello matematico di sviluppo ben supportato può aiutare gli scienziati a rispondere a domande di lunga data sul perché le piante crescono in questo modo. In teoria, se riesci a dimostrare che la crescita avviene a un ritmo prevedibile o secondo un modello geometrico affidabile, puoi iniziare a testare teorie relative al comportamento delle piante rispetto a quel modello per convalidarle .
Sin dai tempi antichi, fisici e architetti, come lo stesso da Vinci, hanno studiato le forme naturali per l’ispirazione. L’ultimo decennio ha visto un’esplosione di ricerca sugli approcci progettuali basati su forme viventi, variamente chiamate design biomeccanico, bioispirato e biofilo. Piuttosto che imitare direttamente gli organismi esistenti, questi approcci utilizzano le leggi osservate, come le spirali di Fibonacci e la regola di da Vinci sopra, per costruire versioni sintetiche che conservano alcuni dei vantaggi strutturali degli originali viventi.
I design basati su queste leggi naturali emergenti hanno anche il vantaggio di essere esteticamente splendidi. Il rapporto aureo, in cui il rapporto dimensionale di una parte con il suo intero è di circa 1:1.618, è famoso fin dai tempi di Euclide come un modo per descrivere la bellezza naturale in qualsiasi cosa, dai dipinti rinascimentali ai volti umani .
L’applicazione della sequenza di Fibonacci ai sistemi di ramificazione aiuta sicuramente a rendere gli alberi e i diagrammi costruiti da Toon un aspetto incredibilmente realistico. Il progetto, chiamato Tree of Water and Power, è attualmente in fase di sviluppo – la prima installazione dovrebbe essere aperta a dicembre 2022 – ma Toon è incoraggiato dall’emergere della famosa sequenza.
“Non l’ho fatto apposta”, ha sottolineato. “Ho appena seguito le regole dell’albero.”